S is a set of points in the plane. How many distinct triangles can be drawn that have three of the points in S as vertices?
(1) The number of distinct points in S is 5.
(2) No three of the points in S are colinear.
Let’s get an idea of what this looks like.
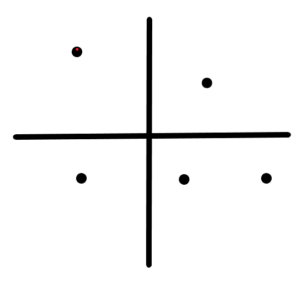
So, here’s the plane and the points. We connect three of the five points to make a triangle:
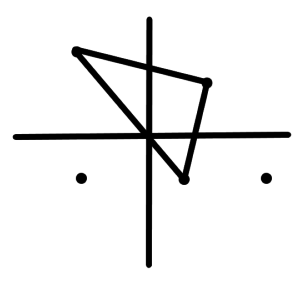
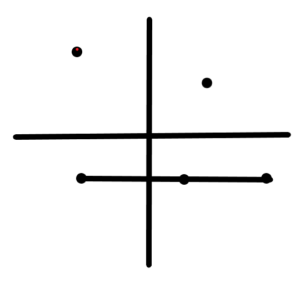
Unless, of course, those three points are on the same line:
Clue (1): This doesn’t tell us than we don’t have three points that form a line, so it’s insufficient. A and D are out.
Clue (2): This eliminates that possibility that three of the points form a line, but we don’t know how many points we’re working with, so it’s insufficient. B is out.
Clues (1) and (2) Together: Now, because no three points are colinear, any selection of three points will form a triangle. How many ways can we select three distinct points from five distinct points? Hopefully, this sort of question is familiar from your study of combinatorics. If so, you know there’s a way to do this, but, because this is data sufficiency, we don’t actually need to do the calculation.
(1) and (2) together are sufficient.
The correct answer is C.