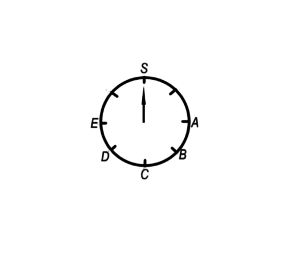
The dial shown above is divided into equal sized intervals. At which of the following letters will the pointer stop if it is rotated clockwise from S through 1,174 intervals?
(A) A
(B) B
(C) C
(D) D
(E) E
This is really a remainder question. If that’s unclear, think about a smaller number of intervals, for example 20. If we pass the pointer through 20 intervals, it will complete 2 rotations (16 intervals) and pass through 4 more, stopping at C. The related calculation is 20 divided by 8 results in a remainder of 4.
Like many GMAT questions, once you get past the language and the context, you end up with a calculation and you have to decide how best to approach the calculation. I’m going to use this distributive property to simplify things considerably and avoid the needlessly complex process of long division.
\(\frac{1174}{8} = \frac{1000 + 160 + 14}{8} = \frac{1000}{8} + \frac{160}{8} + \frac{14}{8}\)
I split the number up so that the large parts, 1000 and 160 are both evenly divisible by 8 (the quotients are 125, and 20, respectively). Now I only need to pay attention to \(\) to find the remainder I’m looking for. When 14 is divided by 8, the remainder is 6. If I count 6 intervals starting at S, moving clockwise, I end up at E.
The correct answer is E.
For most of you, the way I calculated this will seem a bit strange. The become proficient at this will require some work (you must stop yourself every time you start to long divide, or column multiply, and think, “what would John do?”), but the payoff is significant.
SIDE NOTE: If you know the divisibility rule for 8, you can get to the answer even faster:
A integer is divisible by 8 if the last three digits form a number that is divisible by 8.
This works because an integer can be split into a multiple of 1000 and a three-digit number. All multiples of 1000 are divisible by 8 because 1000 is divisible by 8. The three-digit number can be thought of as the left over part with respect to 8. If it is also divisible by 8, the whole number is divisible by 8. If you understand this, you can use it to simply your calculation by only focusing on the last three digits.