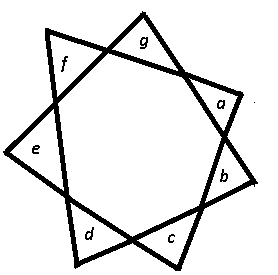
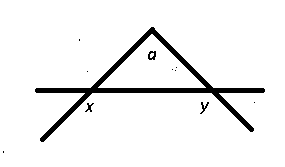
How can you tell the difference between a problem that you can solve with a straightforward application of content knowledge and a problem that requires a more flexible approach?
A good place to start is at the edge of reasonable content knowledge. Let’s say that you’ve been working hard, you feel like you know everything you need to know, your confident that the ratios of the sides of a 30-60-90 triangle will be rattling around in your head when you’re so old that you’re not too sure who the president is, and then… WTF??? You get a problem that, that, that… you don’t even know what to say. You’re on the verge of asking the proctor if this is really the GMAT that you’re taking.
For Example:
In the figure above what is the approximate value of the sum of the angles a, b, c, d, e, f, and g?
(A) 180 (B) 270 (C) 360 (D) 450 (E) 540
Huh? WTF!? Surely there’s a flashcard that I can’t recall. It’s that rule about the interior angle measure of the exterior parts of non-convex polygons, right? Is there such a rule?… Do I really need an MBA?
So, what to do?
Let’s start with what should NOT to:
- Copy the figure on your scratch pad.
- Label the interior angles of the heptagon – t, u, v, w, x, y, and z.
- Break the heptagon up into unique quadrilaterals containing the variable in the original figure and the variables you’ve inserted. (Try it. I double dare you!)
- Use the interior angle measure of a quadrilateral (360) to get a ton of equations
- Take the sum of those equations…
You get the idea.
We need to take more flexible approach. We need to exploit the structure of the test. There is only one answer, and because we don’t have a protractor and a ruler it can’t be dependent on this particular figure. The answer will apply to any variation of the figure. In essence the GMAT is telling you that there is a rule that you can use to answer this question. You don’t have to know the rule, and you don’t have to derive the rule. You just need check that rule with an example.
This figure sucks. Let’s use a regular heptagon. That way the angles a, b, c, d, e, f, and g will be equal and we only need to find one of them.
Now that’s a regular heptagon, the figure above will suffice. The interior measure of a heptagon is 180(7 – 2) = 900 degrees. In a regular heptagon all the interior angles will be equal, so x and y will be 900/7 which is around 128. So the two base angles of the isosceles triangle poking out of the heptagon have measure 180 – 128 = 52. Thus, angle a must be approximately 180 – 2(52) = 76, and the sum of all the angles will be approximately 7(76) = 532. The answer must be E.
In sum, if you are an experienced GMAT’er, and a problem looks too hard (harder than anything you’ve seen before) it might just be an example of a rule that you don’t know. Use an easier, more convenient, example to confirm the rule.
For more examples of this kind of problem, take a look at these PS problems in the 2016 official guide:
Diagnostic Test: 10 (regular pentagon), 23 (use 4*6)
Problem Solving Practice Questions: 23 (10 by 1 by 1), 35 (n = 5 and you’re done), 38 (two examples should so the trick), 44 (k = -1), 60 (k = 1), 112 (Q = 3), 209 (p = 3)